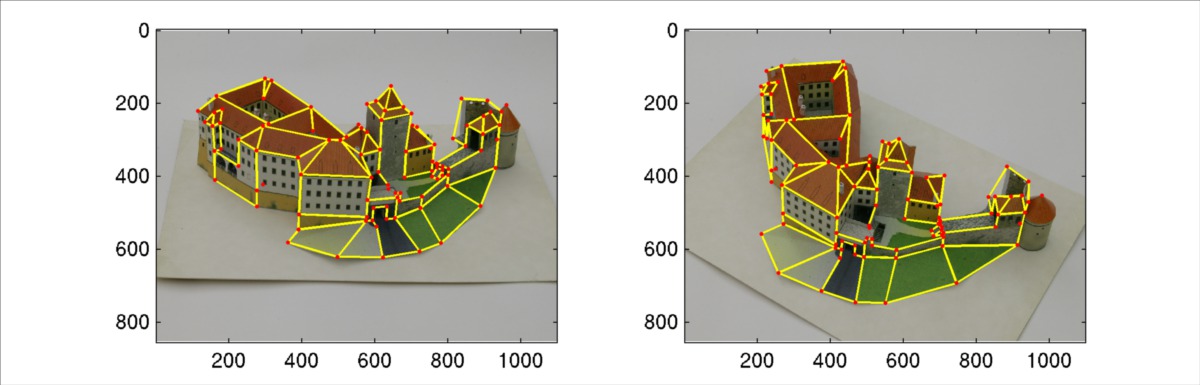
Homework 09 - Metric reconstruction

This homework is split into two weeks.

Essential matrix

Having a fundamental matrix F and camera calibration K, the essential matrix E can be computed from the equation

<latex>F = K^{-\top} E K^{-1}\,.</latex>

First, matrix E1 is computed as: 

E1 = K' * F * K;

Due to errors in data used to estimate F and/or K, the obtained matrix E1 is not a true essential matrix, its two non-zero singular values are not equal. So the matrix must be modified in order to make these singular values equal: 

[U D V] = svd( E1 ); 
D(2,2) = D(1,1);
E = U * D * V';

To summarize, starting with regular matrix G obtained from the 8-point algorithm, we apply SVD two times. First, G is decomposed, the smallest singular value zeroed and F is composed. Secondly, K is applied, E1 is decomposed and the two singular values are made equal giving raise to essential matrix E. Finally, K can be applied to compute a fundamental matrix Fe consistent with K from E.

Steps

Find two essential matrices. A possibly bad Ex and the best E

  1. Compute essential matrix Ex using your best fundamental matrix F estimated in HW-09 and internal calibration K.mat from HW-04. Compute also the fundamental matrix Fx consistent with K from Ex and K
  2. Draw the 12 corresponding points (from HW-09) in different colour in the two images. Using Fx, compute the corresponding epipolar lines and draw them into the images in corresponding colours. Export as 09_egx.pdf.
  3. Draw graphs of epipolar errors d1_i and d2_i w.r.t Fx for all points. Draw both graphs into single figure (different colours) and export as 09_errorsx.pdf.
  4. Find essential matrix E by minimizing the maximum epipolar error of the respective fundamental matrix Fe consistent with K using the correspondences from HW-09:
    1. Generate all (495) 8-tuples from the set of 12 correspondences and estimate fundamental matrix F (via G) for each of them.
    2. For each tested F, compute essential matrix E using internal calibration K.mat from HW-04.
    3. Compute fundamental matrix Fe consistent with K from E and K and its epipolar error over all matches.
    4. Choose the Fe and E that minimize maximal epipolar error over all (i.e. the 12 + the mesh) matches.
  5. Draw the 12 corresponding points in different colour in the two images. Using Fe, compute the corresponding epipolar lines and draw them into the images in corresponding colours. Export as 09_eg.pdf.
  6. Draw graphs of epipolar errors d1_i and d2_i w.r.t Fe for all points. Draw both graphs into single figure (different colours) and export as 09_errors.pdf.
  7. Save F, Ex, Fx, E, Fe and u1, u2, point_sel (same as in HW-09) as 09a_data.mat.

Cameras and reconstruction

  1. Decompose the best E into relative rotation R and translation C (four solutions). Choose such a solution that reconstructs (most of) the points in front of both (computed) cameras.
  2. Construct projective matrices P1, P2 (including K).
  3. Compute scene points X.
  4. Manually create set of at least 30 edges connecting the points. The edges should correspond to real edges in the scene.
  5. Display the images, draw the input points as blue dots and the scene points X projected by appropriate P_i as red circles. Draw also the edges, connecting the reprojected points as yellow lines. Export as 09_reprojection.pdf.
  6. Draw graph of reprojection errors and export as 09_errorsr.pdf.
  7. Draw the 3D point set connected by the edges as a wire-frame model. From the top, from the side, and from some general view. Export as 09_view1.pdf, 09_view2.pdf, and 09_view3.pdf.
  8. Save Fe, E, R, C, P1, P2, X, and u1, u2, point_sel as 09b_data.mat.
Example of the corresponding points and edges Example of a wire-frame model reconstruction

Upload

The first part: upload an archive consisting of:

  1. 09_errorsx.pdf, 09_errors.pdf
  2. 09_egx.pdf, 09_eg.pdf
  3. 09a_data.mat
  4. hw09a.m – your Matlab implementation entry point.
  5. other files required by hw09a.m

The second part: upload an archive consisting of:

  1. 09b_data.mat
  2. 09_reprojection.pdf
  3. 09_errorsr.pdf
  4. 09_view1.pdf, 09_view2.pdf, 09_view3.pdf
  5. hw09b.m – your Matlab implementation entry point.
  6. other files required by hw09.m