Homework 08 - Epipolar geometry

Implementation

[F, G] = u2FG( u1, u2 )

The function u2FG computes the 'fundamental matrix' G using the eight-point algorithm from 8 euclidean correspondences u1, u2, measured in two images. Then the true fundamental matrix F is found, which is close to G and rank(F) = 2.

Normalization

Inside this function, prior to constructing a matrix for SVD, the points must be normalized. This can be done by subtracting a centroid of the 8 points and dividing by it's standard deviation; in each image separately. Express the normalization as homographies H1 and H2, the points are modified by these. 

u1n = H1 * u1p;  % u1p are homogeneous
u2n = H2 * u2p;  % u2p are homogeneous

Then the computed Gn and Fn relate the normalized correspondences u1n and u2n and must be back-normalized. 

G = H2' * Gn * H1
F = H2' * Fn * H1

Imposing Rank = 2

The matrix Gn computed by SVD has usually rank = 3 due to noise in data. Therefore modification to rank = 2 is needed. Compute SVD of the Gn, nullify the D(3,3) and compose the matrix back.

Input Images

daliborka_01 daliborka_23

Steps

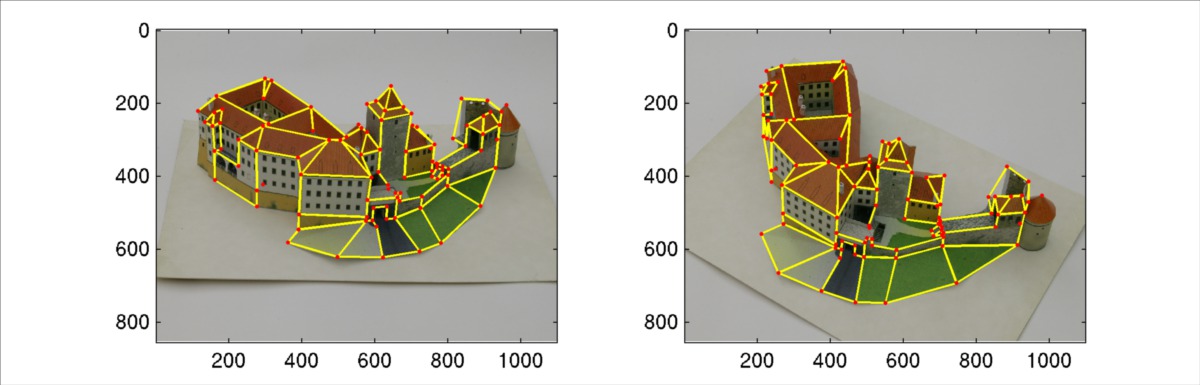
1. Correspondences between the images

  1. Manually obtain a set of 12 image correspondences (matches) between the images above. These correspondences must sufficiently cover whole area of both images as well as the 3D space.
  2. Manually obtain another set of at least 40 correspondences. Choose reasonable vertices (e.g., roof corners) that can be later connected by edges into a wire-frame mesh (for visualization). The edges (together with the vertices) will be used in the next homework. (You do not need to set-up edges now.)
Example: The set of 12 correspondences Example: The mesh (edges not needed now)

2. Epipolar geometry

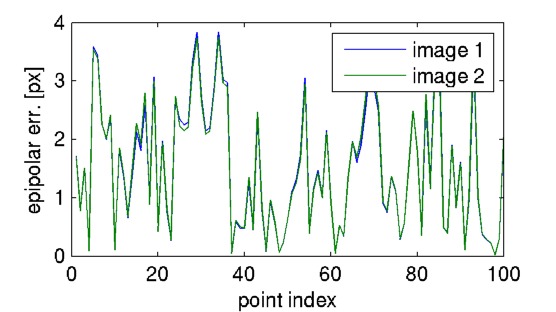
  1. Find the fundamental matrix F relating the images above: generate all (495) 8-tuples from the set of 12 correspondences, estimate (the true) F for each of them and chose the one, that minimizes maximal epipolar error over all (i.e. the 12 + the mesh) matches.
    1. For a particular tested fundamental matrix F, compute epipolar lines l1_i = F'*x2_i and l2_i = F*x1_i (provided that points are homogeneous) for each point i. Then evaluate the Euclidean distances d1_i = d(x1_i,l1_i) and d2_i = d(x2_i,l2_i) in images. The epipolar error for the i-th match is defined as d1_i + d2_i.
  2. Draw the 12 corresponding points in different colour in the two images. Using the best F, compute the corresponding epipolar lines and draw them into the images in corresponding colours (a line segment given by the intersection of the image area and a line must me computed). Export as 08_eg.pdf.
  3. Draw graphs of epipolar errors d1_i and d2_i for all points (point index on horizontal axis, the error on vertical axis). Draw both graphs into single figure (different colours) and export as 08_errors.pdf.
  4. Save all the data into 08_data.mat: all correspondences as u1, u2, the indices of the 12 selected correspondences as point_sel, the 'best' matrices F and G.
Example: the epipolar lines Example: the epipolar error for all points

Upload

Hand an archive consisting of:

  1. 08_eg.pdf
  2. 08_errors.pdf
  3. 08_data.mat
  4. u2FG.m
  5. hw08.m – your Matlab implementation entry point.

any other files required by hw08.m (including data and files from the repository).