Table of Contents

Statistika 2

Program:

Domácí úkol 2

Opakování: pravděpodobnost (2)

Distribuční a kvantilová funkce

(Použití tabulek kvantilů a kritických hodnot)

Hmotnost vyráběné pilulky lze popsat normálním rozdělením se střední hodnotou 120mg a rozptylem 1mg2. Výstupní kontrola testuje, zda tomu tak skutečně je, tak, že “rozumně” velký náhodný vzorek pilulek byl zvážen a setříděn podle narůstající hmotnosti.

V jakém rozmezí lze čekat hmotnost 10% resp. 1% resp. 0,1% nejlehčích pilulek?

V jakém rozmezí asi bude hmotnost 10% resp. 1% resp. 0,1% nejtěžších pilulek?

Jaká je pravděpodobnost, že nalezneme pilulku o hmotnosti 120mg?

Jaká je pravděpodobnost, že nalezneme pilulku těžší než 120mg?

Jaká je pravděpodobnost, že nalezneme pilulku těžší než 123mg?

Jaká je pravděpodobnost, že nalezneme pilulku o hmotnosti nižší než 117,5mg?

Generování (pseudonáhodných)čísel

Jak lze vygenerovat (pseudo)náhodné číslo z normálního rozdělení $N(0,1)$, máme-li k dispozici generátor (pseudo)náhodných čísel z intervalu $(0,1)$? A jak lze vygenerovat číslo z lib. daného rozdělení?

Vztah reálného světa a pravděpodobnosti a statistiky

Ilustrace: 3 světy - reálný, reálný zjednodušený, teoretický pravděpodobnostní model.

Vlastnosti odhadů parametrů rozdělení pravděpodobnosti

Vypočtěte $E(a+BX)$ a $var(a+bX)$, kde $a,b \in \mathbf{R}$ a $X$ je náhodná veličina.

Spočtěte střední hodnotu a rozptyl součtu resp. rozdílu dvou náhodných veličin. Spočítejte obecně a speciálně pro $X,Y \sim N(\mu, \sigma^2)$.

Vysvětlete termíny:

Ilustrace: střelba na terč

Uvažme realizace $x_i, i=1,\ldots,n$ náhodné veličiny z rozdělení $N(\mu,\sigma^2)$ s neznámým parametrem $\mu$ a se známým parametrem $\sigma^2$. Dále mějme čtyři odhady střední hodnoty $\mu$: $m_1=x_1, m_2=x_{(1)}, m_3=\frac{\sum_{i=1}^n{x_i}}{n}$ a $m_4=\frac{\sum_{i=1}^n{x_i}+1}{n}$.

U každého odhadu určete, zda je nestranný, asymptoticky nestranný a konzistentní.

Centrální limitní věta

Jazyk R:

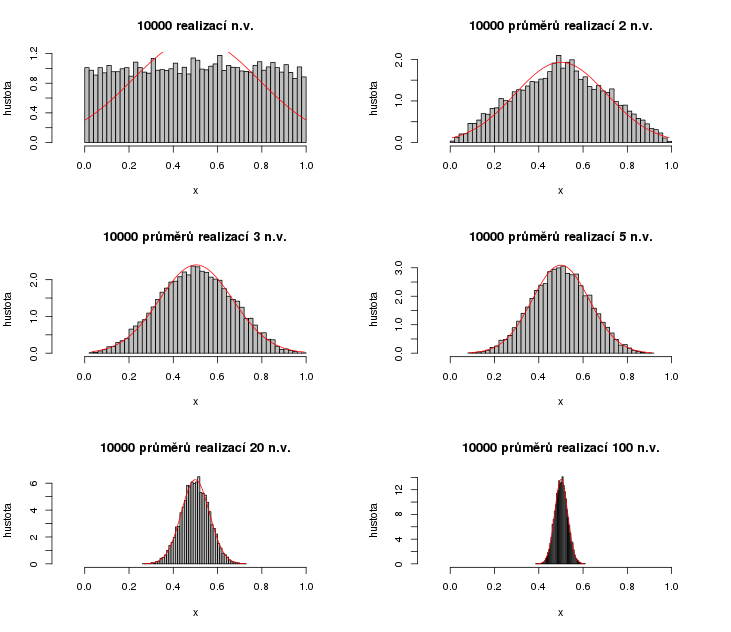
Formulujte a vysvětlete centrální limitní větu a sami si ji vyzkoušejte pomocí následujícího programu v jazyce R.

Dokážete program (funkci g()) upravit tak, aby demonstroval případy, kdy centrální limitní věta “neplatí” (tj. kdy normovaný součet náhodných veličin nemá normální rozdělení)? 

# Demonstrace centrální limitní věty (CLV).
# CLV budeme demonstrovat na 'n' průměrech 'm' relizací náhodné veličiny
# generované funkcí 'g'.

# Funkce generující 'n' realizací náhodné veličiny.
# Argumenty:
#   n: velikost výběru
# Vrací: vektor 'n' realizací náhodné veličiny.
g<-function(n) {
  
  # rovnoměrné rozdělení
  x<-runif(n,0,1)

  # další způsoby generování relizací náhodných veličin jsou 
  # zakomentované (lze je jednoduše aktivovat smazáním znaku '#' před nimi)
  # normální  rozdělení
  #x<-rnorm(n,.5,.2)
  
  # trojúhelníkové rozdělení
  #x<-runif(n,0,.5)+runif(n,0,.5)
  
  # bimodální rozdělení
  #x<-rnorm(n,.75-.5*(runif(n,0,1)<.5),.1)

  # házení mincí (alternativní rozdělení)
  #x<-rbinom(n,1,.5)
  
  return(x)
}

# Funkce generující 'm' náhodných vektorů délky 'n' a vykreslující histogram
# jejich průměrů spolu s proloženým odhadem hustoty pravděpodobnosti 
# normálního rozdělení s parametry odhadnutými z dat.
# Parametry:
#  m - počet vektorů
#  n - délka jednoho vektoru
clv<-function(m,n,titulek) {
  # alokujeme matici typu 'm x n', v 'm' řádcích vektory 'n' realizací náh. veličiny
  x<-matrix(NA,m,n)
  for (i in 1:m) {
    x[i,]<-g(n)
  }
  x<-colMeans(x)
  # histogram
  hist(x, probability=TRUE, breaks=50, col='gray', ylab='hustota',main=titulek)#,xlim=c(-.1,1.1))
  # proložíme hustotu pravděpodobnosti normálního rozdělení
  ax<-seq(from=min(x), to=max(x), length=100) # body na ose x
  ay<-dnorm(ax, mean(x), sd(x))
  lines(ax, ay, col='red')
}

# počet vektorů
m<-100
# délka jednoho vektoru
n<-10000

options(scipen=5) # čísla chceme vypisovat ve fixní notaci

# vykreslíme 3x2 obrázků
opar<-par(mfrow=c(3,2))
clv(1,n,paste(n,'realizací n.v.'))
clv(2,n,paste(n,'průměrů realizací 2 n.v.'))
clv(3,n,paste(n,'průměrů realizací 3 n.v.'))
clv(5,n,paste(n,'průměrů realizací 5 n.v.'))
clv(20,n,paste(n,'průměrů realizací 20 n.v.'))
clv(m,n,paste(n,'průměrů realizací',m,'n.v.'))
par(opar)